Depth | Why is randomness so important for deep learning?
Lei Feng network (search "Lei Feng network" public number attention) by: The author of this article Eric Jang, Google Brain research engineer, the translator is Ren Jiejun and Xu Jun. Has been authorized by the Jiangmen entrepreneurship (thejiangmen).
In a pleasant afternoon, I began to try to explain to my mother in an easy-to-understand language the importance of randomness for deep learning. Although my mother still knows little about deep learning, I think my efforts have been partially successful. I am fascinated with this approach and applied it to my practical work.
I would like to give this small technical article to practitioners in the field of deep learning. I hope that everyone can have a better understanding of the inner workings of the neural network.
If you are a newcomer to entry, then you may feel that a lot of technology is being used on training neural networks, such as dropout regularization, amplification gradient noise, asynchronous random decline. What is the same for these technologies? The answer is that they all use randomness !

Randomness is the key to the normal operation of deep neural networks:
Random noise causes the neural network to produce multiple output results in the single input case;
Random noise restricts the flow of information in the network, prompting the network to learn meaningful data in the data;
Random noise provides "exploration energy" as the gradient falls, allowing the network to find better optimization results.
Single Input Multiple Output (Single In Multiple Output)Let us assume that you are training a deep neural network to implement classification.

For each area in the map, the network will learn to map the image to a series of word tags, such as "dog" or "person."
Such classification performs well, and such deep neural networks do not need to add randomness to the reasoning model . After all, any picture of a dog should be mapped to the word "dog". There is no randomness.
Now let's assume that you are training Go in a deep neural network. In the case of the following figure, the deep neural network needs to drop the first chess piece. If we still use a strategy that determines the invariability, we will not be able to draw a good result. You may ask, why? Because in this case the optimal "first step" selection is not unique, for each position on the board, they have rotational symmetry with the opposite position, so having the same opportunity becomes the better choice. This is a multivariate optimal problem . If the neural network strategy is deterministic and single input/single output, the optimization process will force the network to choose the average position to move to all the best answers, and the result is balanced in the center of the board, which is exactly in the game of chess. It is considered a bad start.

Therefore, randomness is very important for a network that wants to output multivariate optimal estimates instead of repeating the same results over and over again. When the action space implies symmetry, a very critical factor of randomness, with the help of randomness, we can break the symmetric paradox that cannot be solved in the middle of inclusion.
Similarly, if we want to train a neural network to compose or draw, of course we don't want it to always play the same music, depicting monotonously repeated scenes. We look forward to the rhythms of change, the sound of surprises and the creative expression. In a deep neural network combined with randomness, on the one hand, the certainty of the network is maintained, but on the other hand, the output is changed to a parameter of a probability distribution, so that we can use the convolution sampling method to draw a sample with random output characteristics. Example picture.
DeepMind's Alpha Dog adopts the principle that based on a given go board image, the probability of winning each kind of go way is output. This kind of network output distribution modeling is widely used in other deep reinforcement learning areas .
Randomness and Information TheoryWhen I first touched on probability theory and mathematical statistics, I was very tangled in understanding the physical meaning of randomness. When throwing a coin, where does the randomness of the result come from? Is randomness just deterministic chaos? Is it possible to do absolutely random?
To be honest, I still didn't fully understand these issues.

In information theory, randomness is defined as the absence of information. Specifically, the information of an object is the minimum number of bytes that can be described in a computer program. For example, the first one million bytes of π can be represented as 1,000,002 characters in bytes, but it can also be represented in full by 70 characters, as shown by the Leibniz equation:

The above formula is a compressed representation of one million data of π. A more accurate formula can represent the first million data of π as fewer bits. From this point of view, randomness is an amount that cannot be compressed. The first one million of π can be compressed to indicate that they are not random. Empirical evidence shows that π is a normal number and the information encoded in π is infinite.
We now consider using the number a to represent the first trillion digits of π, such as a=3.141592656... If we add a random number r to it (-0.01, 0.01), we will get one at 3.14059... and Number between 3.14259... Then the effective information in a + r is only three digits because the additive random noise destroys the information carried by the digits after the hundred decimals.
Forcing deep neural networks to learn succinct expressionsThis definition of randomness (referring to “randomness is the amount that cannot be compressedâ€, Translator's Note) is related to randomness.
Another way to embed randomness into deep neural networks is to embed noise directly into the network itself, which is different from using a deep neural network to simulate a distribution. This approach makes learning tasks more difficult because the network needs to overcome these inherent "perturbations."
Why do we want to introduce noise in the network? A basic intuition is that noise can limit the amount of information that data can carry over the network.
We can refer to an auto-encoder model. This neural network structure attempts to efficiently encode the input data by “compressing†it, obtain a lower-dimensional representation in the hidden layer, and reconstruct the original data at the output layer. Here is a schematic diagram:

During the training process, the input data passes through the network node from the left and comes out on the right, much like a pipeline.
Suppose we have a theoretically existing neural network that can train on real numbers instead of floating-point numbers. If there is no noise in the network, each layer of the deep neural network actually processes an infinite amount of information. Although the automatic coding network can compress a 1000-dimensional data to 1D, the 1-D number can use real numbers to encode any number of infinite dimensions, such as 3.14159265...
Therefore, the network does not need to compress any data and does not learn any meaningful features. Although computers do not really represent numbers with infinite dimensional accuracy, they tend to give neural networks far more data than we would like.
By limiting the amount of information in the network, we can force the network to learn a concise representation from the input features. There are several ways to do this now:
Variational Automatic Encoding (VAE), which adds Gaussian noise to the hidden layer, can destroy "surplus information" and force the network to learn a concise representation of the training data.
Dropout regularization is closely related to the noise of variational autocoding (which may be equivalent?) - it randomly sets some of the elements in the network to zero so that it does not participate in training. Similar to variational autocoding, dropout noise forces the network to learn useful information in limited data.
A deep network of random depths - Ideas are similar to dropouts, but instead of being set to zero at the unit level randomly, some layers in the training are randomly removed so that they do not participate in training.
One very interesting article is "Binarized Neural Networks". The author uses binary weights and activations in forward propagation, but uses real-valued gradients in backward propagation. Here the noise in the network comes from the gradient—a noisy binarization gradient. Binary Nets do not need to be more powerful than conventional deep neural networks. Each cell can only encode one bit of information. This is to prevent the two features from being compressed into one cell by floating point coding.
A more efficient compression scheme means better generalization of the test phase, which also explains why the dropout is so effective against overfitting. If you decide to use conventional automatic coding instead of variational automatic coding, you must use random regularization techniques, such as dropout, to control the number of bits of the compressed feature, otherwise your network will most likely overfit.
Objectively speaking, I think VAEs have advantages because they are easy to implement and allow you to specify exactly how many bits of information are passed through each layer of the network.
Avoiding local minimums in trainingTraining a deep neural network is usually done by a gradient descent variant, which basically means that the network iterates parameters by reducing the average loss error over the entire training data set. It's like walking from the top of the mountain to the bottom. When you reach the bottom of the valley, you will find the optimal parameters of the neural network.
The problem with this approach is that there are many local minima and plateaus on the loss function surface of the neural network (because the network fitting function is usually non-convex). The loss function of the network can easily fall into a small pit, or fall into a flat area with a slope of almost 0 (local minimum), but you feel that you haven't got a satisfactory result.
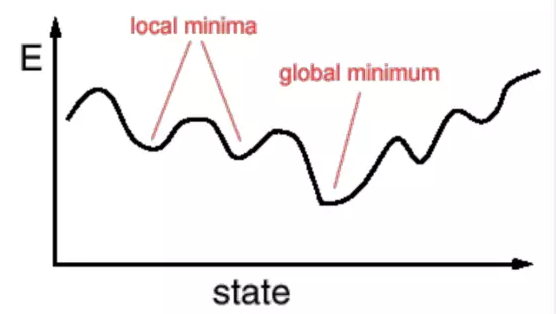
How does randomness help deep learning models? My third explanation is based on the idea of ​​exploration.
Because the data sets used to train deep neural networks are usually very large, if we calculate the gradient for all the gigabytes of data in each gradient descent, this calculation is really too large! In fact, we can use the stochastic gradient descent algorithm (SGD) . In this algorithm, we only need to randomly pick a small part of the data from the data set and calculate its average gradient.
In evolution, if the species's successful continuation is simulated with a random variable X, random mutations or noises increase the variance of X, and their descendants may become far better (adaptability, anti-virus capacity) or far more Poor (weak, weak, infertile).
In numerical optimization, this "gene mutation" is called "thermodynamic energy" or "temperature", which allows the iterative trajectory of the parameter to not always go "down the mountain" but occasionally jump out of the local minimum or pass " Tunnel through the mountain."
These are closely related to the "exploration-mining" balance in enhancing learning. A purely deterministic deep neural network without gradient noise is trained. Its “mining†capability is 0, it directly converges to the nearest local minimum point, and the network is shallow.
The use of stochastic gradients (by adding small samples or adding noise to the gradient itself) is an effective way to allow optimization methods to do some "search" and "jump out" from local minima. The asynchronous random gradient descent algorithm is another possible source of noise that allows multiple machines to compute gradient descent in parallel.
This "thermodynamic energy" guarantees that the symmetry in the early stages of training can be destroyed, thereby ensuring that all gradients in each layer of the network are not synchronized to the same value. Noise not only destroys the symmetry of the neural network in the behavioral space, but also undermines the symmetry of the neural network in the parameter space.
Last thoughtI have found that the phenomenon is very interesting, that random noise is actually helping artificial intelligence algorithms avoid overfitting, helping these algorithms find solution space in optimization or reinforcement learning. This raises an interesting philosophical question: whether the noise inherent in our neural code is a feature, not a bug.
There is a theoretical machine learning problem that makes me very interested: Whether all the neural network training techniques are actually variants of some general regularization theorem. Perhaps theoretical work in the field of compression will really help to understand these issues.
If we verify that the information capacity of different neural networks is compared with the characteristic representations of manual designs, and it is interesting to observe how these comparisons relate to overfitting trends and the quality of gradients. Measuring the information volume of a network trained with a dropout or a random gradient descent algorithm is certainly not worthless, and I think this can be done. For example, to construct a dataset of composite vectors, the information capacity (in bits, kilobytes, etc.) of these vectors is completely known. We can observe how the different structures of the network are combined by combining techniques like dropouts. The data set goes to a generative model.
Nickel Cadmium Alkaline Battery
Taihang Power begin to produce rechargeable battery since 1956, our Nickel cadmium battery capacity range is from 10ah to 1200ah. NICD battery has the properties of rigid construction, long service life,wide work temperature, resistance to overcharge and overdischarge, low self-discharge, high reliability and easy maintenance.
They are widely used as DC power source for railway vehicle, rolling stocks, petrochemical, oil and gas, electricity industries,electrical appliance,telecommunications, UPS, military, AGV,electric power system,wind and solar energy storage system,etc.
Nickel Cadmium Rechargeable Battery,Nickel Cadmium Alkaline Battery,Alkaline Nicd Batteries,Nicd Battery For Ups
Henan Xintaihang Power Source Co.,Ltd , https://www.taihangbattery.com